TRIBUNA de Enrique Castellanos, FRM, MFIA, director del Instituto BME.
Normalmente en los mercados financieros se manejan dos tipos de volatilidades bien diferenciadas: volatilidad implícita y volatilidad realizada.
Volatilidad implícita es la que el mercado espera en un futuro, es una expectativa de volatilidad a un plazo determinado y para su cálculo se utiliza el precio con el que cotizan las opciones en el mercado. Para calcular el precio de una opción es necesario incorporar, dentro de los parámetros de valoración, la volatilidad que se espera que tenga el activo subyacente hasta la fecha de vencimiento. Por esa razón, si compradores y vendedores de opciones se ponen de acuerdo en el precio de la opción, quiere decir que también están de acuerdo con la volatilidad futura del activo subyacente.
Por otro lado, la volatilidad realizada o histórica es la volatilidad que ha tenido el activo subyacente en el pasado más reciente. Normalmente, para su cálculo se utiliza la desviación típica de los rendimientos del activo subyacente los últimos "n” días.
En determinadas situaciones puede no estar muy claro si la volatilidad implícita aumenta porque lo hace la volatilidad realizada o viceversa, pero parece lógico pensar que ambas deben moverse en el mismo sentido. Así suele suceder, sin embargo, no siempre ocurre.
Cuadro 1: volatilidad implícita 30 días (VIBEX) vs. volatilidad realizada 22 sesiones desde 2007 hasta la actualidad
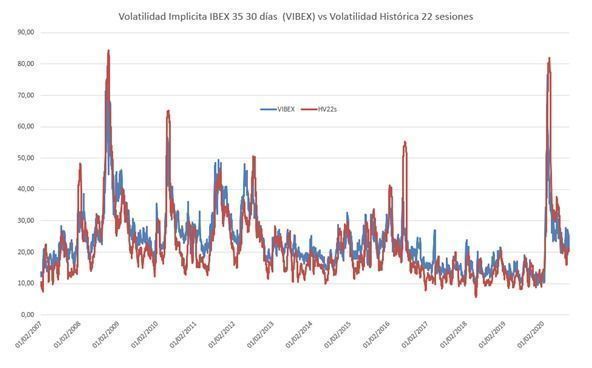
Fuente: elaboración propia a partir de datos de www.meff.com.
En el cuadro anterior podemos observar el movimiento de la volatilidad implícita (VIBEX) y la volatilidad realizada al mismo plazo (un mes). Claramente no son idénticas, aunque sí podemos decir que, normalmente, cuando una aumenta o disminuye, la otra le sigue. Hay tres características más que podemos destacar del cuadro anterior:
- La volatilidad implícita suele ser superior a la volatilidad realizada.
- La volatilidad implícita es más tranquila que la realizada, no sube tanto cuando hay caídas fuertes del mercado.
- No es fácil apreciar en un cuadro con tantos datos históricos, pero ambas volatilidades no siempre se mueven en el mismo sentido. En el siguiente cuadro 2 con el año 2016 en el que tuvimos dos eventos importantes (votación del Brexit y elecciones de EE.UU.) puede apreciarse este efecto.
Cuadro 2: volatilidad implícita 30 días (VIBEX) vs. volatilidad realizada 22 sesiones del año 2016

Fuente: elaboración propia a partir de datos de www.meff.com.
Las estrategias de volatilidad que se suelen utilizar (straddles o conos, strangles o cunas y butterflies o mariposas) se construyen mediante la combinación de posiciones en opciones de un mismo vencimiento y se caracterizan porque variaciones en ambos tipos de volatilidad afectan del mismo modo a cada una de estas estrategias. Por ejemplo, un incremento en la volatilidad implícita y/o realizada favorece a las estrategias compradoras de volatilidad como son la compra de straddle y de strangle y la venta de mariposa.
¿Qué sucede cuando aumenta la volatilidad implícita y se reduce la volatilidad realizada o viceversa? No es muy habitual, pero, en ocasiones, determinados eventos que van a ocurrir en el futuro pueden condicionar al mercado como, por ejemplo, unas elecciones. Antes de las elecciones suele haber incertidumbre que hace que deje de operarse en el mercado, baja la volatilidad realizada, pero como se descuenta que después de ellas el mercado se va a mover con volatilidad, la volatilidad implícita aumenta.
Por esa razón en este artículo explicaremos los calendar spread, unas estrategias que se construyen mediante la combinación de opciones de distintos vencimientos y que permiten tomar posiciones contrarias en la volatilidad implícita y en la realizada.
El más común de los calendar spreads consiste en comprar una opción y vender otra del mismo precio de ejercicio, pero distinto vencimiento (ver cuadro 3). Ambas opciones deben ser call o put:
- C/ Calendar Spread= V/ Opción vencimiento cercano y C/ Opción vencimiento lejano (prima neta a pagar).
- V/ Calendar Spread = C/ Opción vencimiento cercano y V/ Opción vencimiento lejano (prima neta a ingresar).
Cuadro 3: resumen de estrategia calendar spread (time spread)
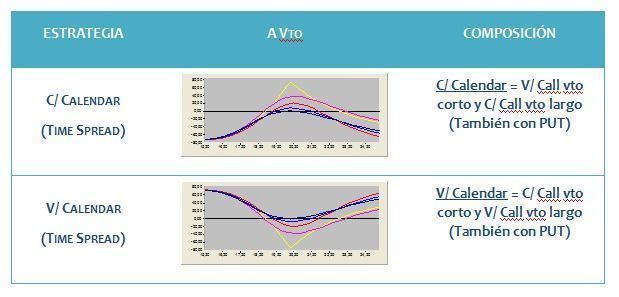
Fuente: elaboración propia.
Los calendar spreads (también llamados time spreads de opciones) son utilizados por los trader con dos objetivos bien distintos:
- Tomar posiciones contrarias en volatilidad implícita y volatilidad realizada.
- Rolar el vencimiento de una determinada posición en opciones (a partir de una posición abierta, se quiere cerrar dicha posición en ese vencimiento y abrirla en uno posterior).
Rolar una opción no es en sí ninguna estrategia, tan solo es un medio de prolongar la vida de una opción de la manera más eficiente posible. Por tanto, nos centraremos en explicar el calendar spread como estrategia de volatilidad.
Aunque en la mayoría de los calendar spread se compran y se venden el mismo número de opciones, un trader podría desequilibrar la estrategia comprando o vendiendo un número mayor de contratos para transformarla en alcista o bajista. Por el momento asumiremos que el número de opciones compradas y vendidas coinciden, obteniendo una estrategia neutral en tendencia (delta neutral).
Cuadro 4: compra de calendar a vencimiento de la opción de más corto plazo
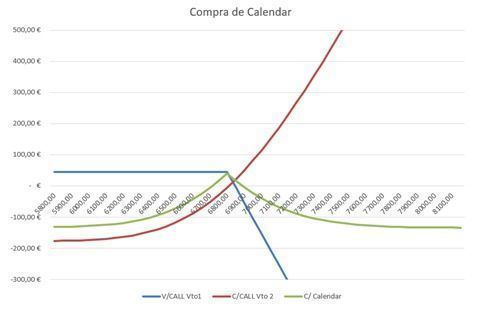
Fuente: elaboración propia.
Cuadro 5: venta de calendar a vencimiento de la opción de más corto plazo
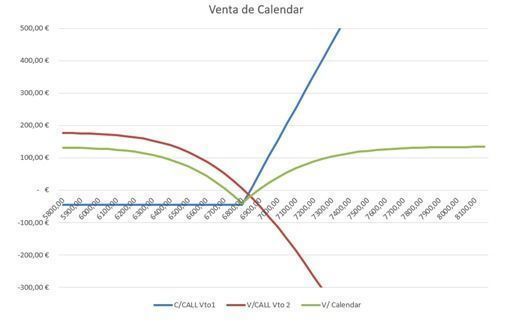
Fuente: elaboración propia.
Veamos un ejemplo de compra de calendar con opciones ATM de IBEX 35.
Cuadro 6: ejemplo de compra de calendar spread
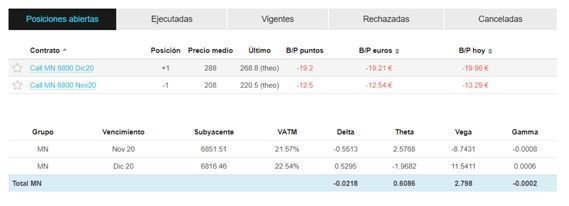
Fuente: elaboración propia.
La estrategia compra de calendar implica tomar una posición con respecto a dos variables distintas: el movimiento del activo subyacente (volatilidad realizada) y el movimiento de la volatilidad implícita.
Movimiento del activo subyacente
Al analizar las sensibilidades del conjunto de la estrategia, los valores theta positivo y gamma negativo se interpretan como un beneficio ante el paso del tiempo y la estabilidad del activo subyacente. Ambas variables son máximas para la serie ATM y aumentan conforme se aproxima la fecha de vencimiento (ver cuadro 7), por lo que serán mayores en valor absoluto para la posición tomada en el corto plazo, la opción vendida. Así, la opción comprada en el vencimiento lejano se verá perjudicada por el paso del tiempo, pero esta pérdida se compensará con creces con el beneficio que le supone a la posición vendedora en el vencimiento cercano, ya que esta perderá valor temporal más rápidamente.
Cuadro 7: compra de calendar y efecto del paso del tiempo
(La línea más plana es la de 38-66, es decir, quedan 38 días al vencimiento de la opción de corto plazo y 66 días a la opción de largo plazo)
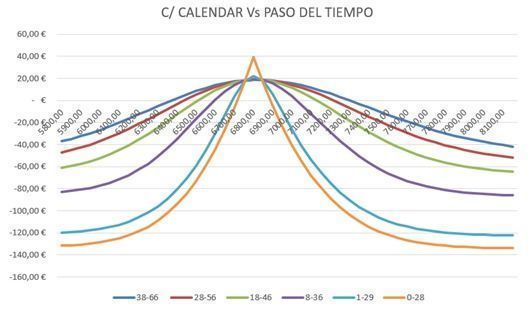
Fuente: elaboración propia.
Movimiento de la volatilidad implícita
La sensibilidad vega positiva de este calendar comprado se interpreta como un beneficio de la estrategia ante un aumento de la volatilidad implícita (ver cuadro 8). Vega es máximo para la serie ATM y disminuye conforme se aproxima la fecha de vencimiento. Así, la posición compradora en el vencimiento lejano se beneficia de un incremento en la volatilidad implícita en mayor medida del perjuicio que este supone para la posición vendedora en el vencimiento cercano.
Cuadro 8: C/ calendar y cambio de la volatilidad implícita
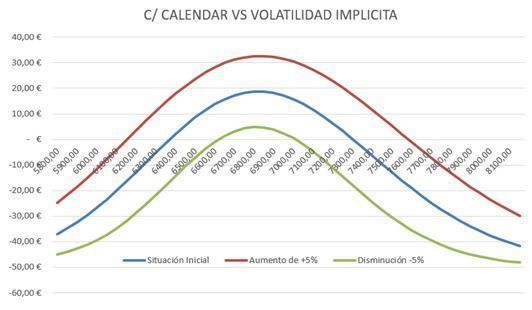
Fuente: elaboración propia.
Movimiento de la estructura temporal
Este caso es un poco más difícil de ver, pero es muy interesante, ya que la opción comprada, como es la de vencimiento superior, le afecta más la volatilidad que a la vendida que es de menor plazo. Un aumento de la pendiente temporal (contango) generará un beneficio para la posición, mientras que lo contrario (backwardation) generará pérdidas
Cuadro 9: C/ calendar y estructura temporal
(Contango de +5% significa que la opción de vencimiento largo tiene un 5% más de volatilidad que la de vencimiento corto)

Fuente: elaboración propia.
Esta sería la posición que podríamos tomar de cara a unas elecciones en las que haya mucha incertidumbre, siempre y cuando se haga con antelación suficiente. Normalmente los mercados se tranquilizan los días antes, pasan los días con mercados bastante laterales, mientras que sube la volatilidad implícita. En esta situación de incertidumbre normalmente la pendiente temporal se empina (contango) mucho. Una vez el mercado ya se encuentra en esa situación de espera de noticias, la posición probablemente debería ser la contraria, ya que el mercado seguramente se moverá, la volatilidad implícita se relaje y se aplane también el contango, incluso si el mercado cae lo suficiente, podría ponerse en backwardation.

